Ahora, nos empezaremos a acercar al Teorema Fundamental del Cálculo, el cuál es el más importante de esta área de estudio, pues establece la relación entre las dos ramas del Cálculo, el Cálculo Diferencial y el Cálculo Integral.
Antes de ello, necesitaremos definir una función muy particular, que nos será de gran importancia.
Consideremos una función f continua en el intervalo [a,b].
Definimos una nueva función A, de la siguiente manera:
Observemos que la función A, sólo depende de la variable x, que es el límite superior de una integral definida. La variable x varía entre a y b.
Si x toma un valor fijo, entonces la integral definida, y por lo tanto la función A, asume un valor bien definido. Por lo tanto, si x varía, el valor de la integral definida también lo hace y define a una función de x, A(x).
A la función A(x), la denominaremos Función Integral o Función de Acumulación.
Notar que, si x=a entonces
Y si x=b, entonces
Interpretación de la Función Integral.
Si f es una función positiva, entonces la función A, puede interpretarse como el área bajo la gráfica de f desde a hasta x, donde x varía entre a y b. Lo veamos gráficamente:


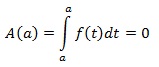

Muy buena entrada!!. Me preguntaron por el Teorema Fundamental del Cálculo en el miniforo, y aconsejé este Blog para salvar las dudas.
ResponderEliminarTal vez tengas que colocar un miniforo?. O bien preguntar algunas cositas luego que hagas las entradas correspondientes. Solo es una sugerencia.