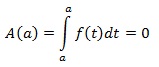Nos acercamos a la noción de derivada. Segunda parte

La Función Integral

Ahora, nos empezaremos a acercar al Teorema Fundamental del Cálculo, el cuál es el más importante de esta área de estudio, pues establece la relación entre las dos ramas del Cálculo, el Cálculo Diferencial y el Cálculo Integral.

Antes de ello, necesitaremos definir una función muy particular, que nos será de gran importancia.

Consideremos una función f continua en el intervalo [a,b].

Definimos una nueva función A, de la siguiente manera:

Observemos que la función A, sólo depende de la variable x, que es el límite superior de una integral definida. La variable x varía entre a y b.

Si x toma un valor fijo, entonces la integral definida, y por lo tanto la función A, asume un valor bien definido. Por lo tanto, si x varía, el valor de la integral definida también lo hace y define a una función de x, A(x).

A la función  A(x), la denominaremos Función Integral o Función de Acumulación.

Notar que, si x=a entonces

Y si x=b, entonces

Interpretación de la Función Integral.

Si f es una función positiva, entonces la función A, puede interpretarse como el área bajo la gráfica de f desde a hasta x, donde x varía entre a y b.  Lo veamos gráficamente:

Propiedades de la Integral Definida

1.Aditividad del intervalo

Si f es integrable en el intervalo [a,b], entonces si c es un punto cualquiera interior al intervalo, tenemos que:

Veamos una interpretación geométrica, considerando una función f positiva, donde a<c<b.

2.Teorema del valor medio (para funciones continuas)

Si f es continua en [a,b], entonces existe un punto c interior al intervalo para el cual se cumple:

f(c) es el valor medio de f en [a,b]

Veamos una interpretación geométrica...
Otros dos resultados, y que no es dificil darse cuenta de los mismos son:

3.

 

4.

 

Los veamos gráficamente...

La Integral Definida

Vimos que el cálculo integral tiene sus orígenes en problemas de cuadraturas en los que se trataba de calcular áreas de regiones planas limitadas por una o varias curvas, por ejemplo como las que mostramos en las figuras:

Nos propusimos calcular el área de regiones de este tipo. Puesto que, en general, la región del plano, bajo la gráfica de la función f,  no puede descomponerse en triángulos o rectángulos (lo que si se puede hacer por ejemplo en el caso de la segunda figura de arriba), vimos que no hay una fórmula que nos permita calcular directamente su área. La idea fue entonces dar soluciones aproximadas que luego, nos permitieron definir el valor exacto del área de la región.

Concepto de Integral Definida

Ahora consideremos a f una función definida en el intervalo cerrado [a,b]. Llamamos recinto S, a la región del plano limitada por la gráfica de la función f, el eje de las abscisas, y las recta de ecuaciones x=a y x=b.

El área buscada se puede aproximar por rectángulos de la siguiente forma:

Primero, se divide el intervalo [a,b] en un número finito de subintervalos [x_k-1,x_k], con 1≤k≤n, cuyas longitudes pueden ser distintas y con la única condición de que no se superpongan, es decir que: 

a=x₀<x₁<…<x_n-1<x_n=b

Se dice que éstos puntos constituyen una partición P del intervalo [a,b]. Cada uno de estos subintervalos tiene una longitud dada por:

 

Si elegimos en cada uno de éstos subintervalos [x_k-1,x_k] un punto arbitrario c_i, podemos calcular el área aproximada de la región S, como sigue:

 

La cual se denomina suma de Riemman de la función f, correspondiente a la partición P.

La norma de la partición P es el máximo del conjunto formado por las longitudes de los subintervalos correspondientes a la partición P. La denotaremos por lPl.

Si existe el límite: 

 

se dice que f es integrable en [a,b]. Además, se llama Integral Definida (o integral de Riemman) de f entre x=a y x=b al valor:

Algunas consideraciones acerca de la definición

Los números a y b, se denominan límites de integración, a es el límite inferior y b es el límite superior.

La integral definida  es un número, no depende de x. De hecho, podríamos cualquier letra en lugar de x sin cambiar el valor de la integral:

De acuerdo a lo visto en las entradas previas, vemos que la integral definida se puede interpretar como el área bajo la curva y=f(x) desde x=a a x=b.

Si f toma valores positivos y negativos como en la figura que se muestra, la integral definida se puede interpretar como un área neta, es decir una diferencia de áreas:

donde A₁ es el área de la región arriba del eje x y debajo de la gráfica de f, y A₂ es el área de la región abajo del eje x y arriba de la gráfica de f.

Aún, cuando hemos definido la integral definida, dividiendo en subintervalos de longitudes desiguales el intervalo [a,b], en muchas situaciones es ventajoso trabajar con subintervalos de igual longitud.

Hemos definido la integral definida para una función integrable, pero no todas las funciones son integrables, el siguiente teorema no ayudará a evitar ciertos conflictos...

Interpretación Geométrica de la Integral Definida

En el siguiente Applet, te presento la interpretación geométrica del concepto de la Integral Definida. En el mismo te presento una definición alternativa, el de las Sumas Superiores y de las Sumas Inferiores. Si surgen algunas dudas, revisa la diapositiva que antecede ésta entrada. 

El problema del Cálculo de Áreas

Integrales Indefinidas

Dentro del estudio de las matemáticas, se trabajan con distintas operaciones que tienen su correspondiente operación inversa, como por ejemplo, adición y sustracción, multiplicación y división, potenciación y extracción de raíces, entre otras.

Hasta ahora, nosotros sabemos resolver el problema de: dada una función f , hallar su derivada, lo cual nos llevó a definir derivada de una función en un punto y estudiar el proceso de derivación.

Pero, muchas de las aplicaciones importantes del cálculo se relacionan con el problema siguiente: dada la derivada de una función, hallar la función que le dio origen a tal derivada. O sea, estamos planteando el problema inverso al de determinar derivadas. Esto es lo que se denomina, determinar la anti-derivada o primitiva de una función. 

Sea f:R->R, una función definida en un conjunto D, la función F es una anti-derivada o primitiva de la función f si y solo si F es derivable en D y F´(x)=f(x)  para todo punto del dominio de f.

O sea:

Ejemplo:

Encuentre una primitiva de la función:

en el conjunto de los reales.

Entonces, debemos buscar una función F que satisfaga que:

Por nuestras experiencias en el proceso de derivación, sabemos que  

tiene por derivada a f(x) , por lo que F sería una primitiva de f.
Otras primitivas de la funcion f, son

Pues vemos que ambas tienen por derivada a f(x) .

Se debe recordar que dos funciones que difieren en una constante tienen igual derivada, por lo que si F es una primitiva de f, también lo será entonces F(x)+C para todo número real C . Es por ello, que se ha usado en la definición anterior la expresión “una primitiva” y no “la primitiva” de f(x).

Veamos una definición...

Dada la función f(x) , se llama Integral Indefinida de f al conjunto de todas sus primitivas y se denota por:

Geométricamente representa una familia de curvas que son paralelas entre sí.

El proceso de encontrar la primitiva de una funcion, es un arte que depende de la experiencia y de la práctica. Por suerte, existen ciertas técnicas o métodos de integración, las cuales pueden reducir sustancialmente nuestro trabajo. 
A continuación, te presento un documento, para que puedas familiarizarte más con los métodos de integración. para leerlo, haz clic aqui.

Nos acercamos a la noción de derivada de una función...

En la siguiente presentaciñon, te daré a conocer una muy buena aproximación al concepto de la Derivada de una función en un punto. La misma, está basada en el problema geométrico de determinar la tangente a una curva.

Puedes profundizar más aún tus conocimientos e ideas, consultando los siguientes documentos:

Derivada y Diferencial - Aplicaciones de la derivada.

Ambos, fueron escritos por la Profesora María de las Mercedes Moya, profesora adjunta de la cátedra Análisis Matemático I, que se dicta en la Facultad de ciencias Exactas de la Universidad Nacional de Salta, República Argentina; a quien agradezco su colabaración.
A continución, te presento la siguiente construcción con GeoGebra, a modo de que puedas comprender mejor la interpretación geométrica del concepto de derivada de una función.

Cuando el límite no existe...

Recordemos una vez más la definición de límite finito:

Para que una función f no tenga límite en el punto x=a, la definición anterior no debe cumplirse para ningún número real L. Entonces si negamos la definición anterior obtenemos que:

Una función f, no tiene límite en el punto x=a si y solo si

Gráficamente, lo anterior siginifica, que para cualquier número L que se proponga como posible límite de la función f en el punto x=a, siempre es posible encontrar una entorno de L talque, en cualquier entorno reducido del punto x=a, hay por lo menos un x del dominio, para el cual f(x) queda fuera del entorno de L .

La siguiente construcción te ayudará a profundizar ésta idea.

Límite de una Función

El concepto de límite es la base fundamental con la que se construye el cálculo infinitesimal (diferencial e integral). Informalmente hablando se dice que el límite es el valor al que tiende una función cuando la variable independiente tiende a un número determinado o al infinito.

Antes de empezar trabajemos con el siguiente ejemplo que nos ayudará a aproximarnos a la idea de límite.

Sean la función definida por la forma:

Sea x=2 un punto de acumulación de su dominio.

En la tabla adjunta escribimos algunos valores para la variable independiente x, en el entorno de 2, y calculamos los valores correspondientes de la función  f:

Observemos ahora la siguiente tabla:

De lo anterior se deduce intuitivamente que el límite de la función  f (x) cuando x tiende a 2, es 5.

Ahora, pasamos a dar la definición formal de límite.

Definición (épsilon-delta) de limite de una función en un punto. 

Sea f:R->R, una función definida en algún subconjunto del conjunto de los números reales, sea x=a un punto de acumulación de su dominio y sea L un número real. Se dice que L es el límite de la función f cuando x tiende a a , y se escribe:

si y solo si se cumple que:

Interpretación geométrica del concepto de límite.

En la siguiente construcción podrás ver la interpretación geométrica del concepto de límite, para la función del ejemplo analizado:

Funciones de Variable Real

Quizás en muchas ocasiones escuchaste las siguientes afirmaciones:

• El precio del helado está en función de su cantidad.
• El espacio recorrido está en función de la velocidad.
• La presión atmosférica es función de la altura.

Estas situaciones ilustran muy bien lo que es una función en matemática, las situaciones de arriba se pueden traducir en la siguiente correspondencia:

• A cada balde con capacidad para una cantidad determinada de helado, le corresponde un único precio.
• A cada velocidad, le corresponde un espacio recorrido, en un intervalo de tiempo determinado.
• A cada altura le corresponde una presión atmosférica.

A esta asignación (o correspondencia) se le llama Función. Al conjunto de elementos a los que se les asigna algo se llama conjunto de definición de la función.

Las funciones se utilizan como modelos de situaciones del mundo real, incluyendo aquellas que son resultado del avance tecnológico, y tienen enorme aplicación en la descripción de fenómenos físicos Por esto se destaca el poder de las funciones tanto para describir de manera simple situaciones complejas como para permitir la predicción de resultados. Puntualmente el concepto de función es unificador en la matemática, ya que aparece en todas sus ramas relacionando variables: entre conjuntos de puntos, entre conjuntos numéricos, etc.

Las funciones son de mucho valor y utilidad para resolver problemas de la vida diaria, problemas de finanzas, de economía, de estadística, de ingeniería, de medicina, de química y física, de astronomía, de geología, y de cualquier área social donde haya que relacionar variables.

Pero… ¿Qué es una función?

Una función es una correspondencia entre dos conjuntos A y B, donde a cada elemento del conjunto A, le corresponde un único elemento del conjunto B. A es el conjunto de definición de la función o dominio y B el conjunto de llegada o codominio.

Los conjuntos A y B deben ser no vacios, y no necesariamente deben ser conjuntos numéricos, pueden ser conjuntos de elementos de diferente naturaleza, por ejemplo, en la función “a cada habitante de la ciudad de Salta le corresponde su número de documento”, el conjunto A o dominio es el conjunto de habitantes de la ciudad de Salta.

Las funciones que más nos van a interesar en matemática son aquellas que asignan a cada número de un cierto conjunto de números otro número. Estas son las funciones numéricas. Es decir en este caso, los conjuntos de definición y de llegada son conjuntos de números.

Así si por ejemplo tomamos la función que “a cada número real x le asigna su doble”, el dominio de ésta función es el conjunto de los números reales y su codominio será el mismo conjunto. A ésta función la podemos escribir de diferentes maneras:

 

O bien como:

 

La letra f simboliza la asignación, la x representa los distintos elementos del conjunto de definición, se le suele llamar también variable independiente, al valor y=f(x) se le suele llamar variable dependiente (la notación y=f(x) indica que el valor de la variable y depende o está en función del valor de x).

A muchas de la funciones que se definen en matemática, se la puede representar gráficamente, utilizando un sistema de coordenadas, en nuestro ejemplo, utilizamos el sistema de coordenadas cartesianas para representa la función f(x)=2x .

Obtenemos el siguiente gráfico:

En matemática, existen gran cantidad de tipos de funciones, las que a nosotros nos interesaran serán entre otras:

Te invito, para que profundices los temas que nos será de interés, que sigas los siguientes links:

Aquí, podrás prufundizar un poco más el concepto de función, ademas podrás realizar el estudio de algunas funciones particulares y de sus gráficas. 

En éste sitio, podrás explorar algunos conceptos que te ayudarán a afianzar el tema y probar tus conocimientos con algunos ejercicios interactivos.  Además te presento un útil graficador de funciones.